5.9 쿼크의 계열

목차 ／ 제5장: 미시적 입자

한 문장 요약:
**에너지 스레드 이론(EFT)**에서는 쿼크를 점으로 보지 않고, “극소 스레드 핵”과 “색 채널”로 이루어진 개방형 단위로 묘사합니다. 핵은 매우 짧고 조밀한 매듭으로서 키랄리티를 정하고 스핀과 자기 지지 에너지의 일부를 담당합니다. 색 채널은 **에너지 바다(Energy Sea)**에서 끌어낸 고장력의 회랑이며, 실체적 관이나 두 번째 스레드가 아닙니다. 다른 쿼크와 결합하여 에너지 장부가 닫힐 때에만 안정화됩니다. 따라서 오래 존재하는 것은 전체적으로 무색인 합성체(메손, 바리온, 글루온이 풍부한 결합 상태)이며, 단독 쿼크는 거시적 규모에서 분리되지 않습니다. 이하에서는 약어 대신 에너지 스레드 이론이라는 표기를 사용합니다.

I. 최소 물리상: 핵 + 색 채널(세 가지 색 = 서로 대체 가능한 세 경로)

• 스레드 핵
  **에너지 스레드(Energy Threads)**가 에너지 바다 안에서 이루는 미세한 매듭입니다. 키랄리티를 정하고 스핀과 관성(자기 지지 에너지)에 기여합니다. 플래이버(up, down, strange, charm, bottom, top)의 차이는 감김 차수와 위상 모드의 차이로 이해할 수 있습니다.
• 색 채널(색 스레드 회랑)
  끌려 나오는 것은 스레드의 몸체가 아니라, 핵의 색 포트가 바다 속에 장력 회랑을 여기합니다. ‘색’은 서로 독립이지만 대체 가능한 세 방향 경로를 뜻합니다.
  구속의 방향성: 합성체에서 세 방향 벡터의 합이 0(무색)이 되면 원거리장이 닫히고, 구조가 안정화됩니다.

보충: 색 회랑은 실체 물체가 아니라 장력이 걸린 공간상의 방향성 띠입니다. 글루온은 이 회랑을 따라 이동하는 위상·에너지 패킷으로, 교환이나 재결합 사건으로 나타납니다. 작은 구가 아닙니다.

II. 구속의 구체화: 단독 쿼크가 보이지 않는 이유

떼어 놓은 두 쿼크가 고장력 회랑으로 연결되어 있다고 가정합니다.

• 더 멀리 끌수록 비용이 늘어납니다: 회랑의 장력은 거의 일정하므로 에너지는 거리와 함께 거의 선형으로 증가합니다.
• 더 저렴한 출구: 임계값을 넘으면 에너지 바다가 중앙 부근에서 재결합하여 쿼크–반쿼크(q–q̄) 쌍을 핵생합니다. 긴 회랑은 두 개의 짧은 회랑으로 나뉘고 각각이 메손으로 닫힙니다.

결론: 관측되는 것은 제트와 ‘메손 비’이며, 단독 쿼크를 뽑아내는 현상이 아닙니다.

III. 하드론의 조립: 메손, 바리온, Y형 닫힘

• 메손(q + q̄)
  거의 직선의 색 회랑이 두 핵을 도킹시키며, 전체가 무색이 됩니다.
• 바리온(q + q + q)
  세 색 회랑이 공간의 Y 접합부로 수렴합니다. 이는 삼각형 둘레보다 에너지 비용이 낮습니다. 세 방향 벡터의 합이 0이 되어 구조가 닫힙니다.
• 글루온 교환
  위상/플럭스 패킷이 회랑을 달리며 세 경로 사이에서 점유를 넘겨줍니다. 색의 교환으로 관측됩니다.

IV. 플래이버(up, down, strange, charm, bottom, top): 감김 차수와 수명

• 감김 차수나 모드가 높을수록 핵생 비용이 커집니다. 입자는 더 무겁고 수명이 짧아지며, 더 낮은 차수로 붕괴하기 쉽습니다.
• 탑 쿼크는 매우 무겁고 매우 빠르게 붕괴하므로, 종종 하드론화가 이루어지지 않습니다. 관측과 부합합니다.

V. 질량·전하·스핀: 장부가 맞춰지는 곳

1. 질량: 두 개의 항목
   • 핵의 자기 지지 에너지(굽힘/비틀림).
   • 색 회랑에 저장되는 장력 에너지(회랑의 ‘에너지 재고’).
     이로써 “양성자 질량의 대부분은 강한 상호작용에서 온다”는 말이 구체화됩니다. 가느다란 회랑의 장력이 쿼크의 ‘나체 질량’을 크게 상회합니다.
2. 전하(왜 1/3의 배수인가)
   쿼크의 전자기적 겉모습은 핵 주변의 방향성 분극에서 비롯됩니다. 이 방향성 예산의 일부가 색 회랑에 소모되므로, 전자기적 투영이 분수 단위로 나타납니다. up 계열은 더 많이 남기고(+2/3), down 계열은 적게 남깁니다(−1/3).
   수치 정합성: 전하는 정확히 ±1/3, ±2/3에 일치합니다. 여기서는 상을 구체화하여 설명할 뿐, 수치는 바꾸지 않습니다.
3. 스핀(누가 얼마나 기여하는가)
   핵의 전체 비틀림, 회랑 내부의 비틀림 파와 글루온의 각운동량이 합쳐져 유효 스핀이 됩니다. 하드론마다 내부 배분이 달라, 쿼크 스핀이 전체의 일부에 그친다는 실험적 분해를 설명합니다.

VI. 스케일 거동: 짧은 거리에서는 거의 자유, 먼 거리에서는 강한 결속

• 아주 짧은 거리(높은 Q²)
  핵이 가까워지면 회랑의 단면이 넓어지고 임피던스가 낮아집니다. 교환은 **‘광대역 터널’**처럼 보이며, 쿼크는 거의 자유(점근적 자유)로 보입니다.
• 멀리 당김(낮은 Q²)
  회랑은 더 가늘고 더 팽팽해지고, 에너지는 거리와 대략 비례하여 증가합니다. 계는 절단과 쌍 생성으로 치우치며, 닫힌 하드론 상태로 되돌아갑니다(구속).

이처럼 점근적 자유와 구속은 같은 에너지 장부의 양면입니다.

VII. 표준모형과의 대응(대립이 아니라 용어의 다리 놓기)

• 세 가지 색 ↔ 세 방향의 회랑(색 경로의 기하학적 가시화)
• 글루온 ↔ 회랑을 달리며 점유를 전달하는 위상/플럭스 패킷(구가 아님)
• 구속과 제트 ↔ 거리와 함께 선형으로 증가하는 에너지 + 재결합에 의한 쌍 생성
• 하드론 내부 ↔ 직선 회랑으로 닫히는 메손, Y 접합으로 닫히는 바리온
• 질량의 주된 근원은 강한 상호작용 ↔ 회랑 장력 + 핵의 자기 지지 에너지가 지배적
• 분수 전하 ↔ 근거리장의 분극이 색 회랑에 소모된 뒤 전자기적으로 투영된 결과
• 탑 쿼크의 비(非)하드론화 ↔ 핵생 시간이 붕괴 시간보다 김

VIII. 경계 조건(기존 데이터와 합치하는 핵심 항목)

• 심부 비탄성 산란(DIS)과 파톤 상
  높은 Q² 및 DIS에서는 설명이 파톤 관점으로 수렴합니다. 기정의 **파톤 분포 함수(PDF)**와 스케일링 법칙은 유지됩니다.
• 전자기적 일관성
  전하 값은 ±1/3, ±2/3에 머뭅니다. 형상 인자와 그 에너지 의존성은 측정과 부합합니다.
• 분광과 하드론화
  공명 스펙트럼, 제트 위상 공간, 분열 함수는 오차 대역 안에 머뭅니다. ‘선형 퍼텐셜 + 쌍 생성에 의한 절단’이라는 직관적 서술이 가짜 피크를 만들어서는 안 됩니다.
• 보존 법칙과 동적 안정성
  색, 플래이버, 에너지, 운동량, 각운동량, 바리온 수의 보존은 엄격히 만족됩니다. 인과 역전이나 자기 증폭 불안정은 없습니다.
• 가시화 ≠ 수치 변경
  회랑/패킷/Y 접합 같은 비유는 직관의 번역일 뿐이며, 매개변수와 **적합(fit)**은 바뀌지 않습니다.

요약하면
쿼크는 스레드 핵과 색 채널로 이루어집니다. 색 채널은 에너지 바다에서 끌어낸 고장력 경로로, 여러 핵을 무색의 전체로 잠급니다. 더 당길수록 비용이 증가하며, 끝내 재결합이 새 쌍을 만들어 계가 닫힌 하드론으로 되돌아갑니다. 그래서 우리가 보는 것은 제트와 하드론이며 단독 쿼크가 아닙니다. 질량, 스핀, 분수 전하도 이 구체적 지도 위에서 제자리를 찾습니다.

도해

1. 단일 쿼크 유닛(핵 + 형성 중인 회랑)

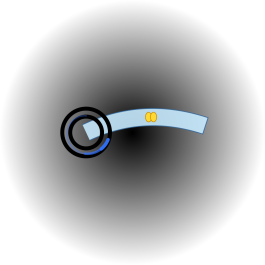
• 요지: 단독 쿼크는 개방되어 있으며, 안정화에는 타자와의 도킹이 필요합니다.
• 독해용 기준: 이중 고리 = 핵, 연한 호 = 색 회랑, 노란색 = 글루온 패킷, 회색 그라데이션 = 얕은 분지.
• 글루온: 회랑을 따라 이동하는 ‘땅콩’형 노란 패킷은 위상·에너지 패킷(교환/재결합 사건)을 뜻하며, 구가 아닙니다.
• 위상 전면: 핵 위의 짙은 파란 호(선단을 두껍게)는 위상 고정을 나타냅니다.
• 본체: 왼쪽의 핵(이중 고리로 그린 자립 중심), 오른쪽으로 뻗는 연한 호가 색 회랑(장력 띠, 실체 관 아님)입니다.

2. 메손(q + q̄, 직선 회랑으로 닫힘)

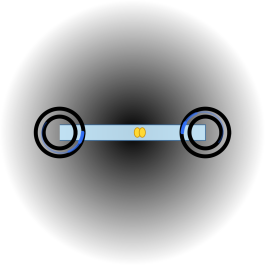
• 요지: 메손은 **‘한 줄 직선 회랑’**이 양끝에서 닫힌 형태입니다.
• 기준: 끝의 이중 고리 = q와 q̄의 핵, 중앙의 연한 띠 = 회랑, 노란 패킷 = 글루온, 전기 화살표 없음(무색).
• 위상 전면: 양끝의 파란 호, 중앙의 노란 패킷은 색 교환을 가리킵니다.
• 본체: 양끝의 핵을 거의 직선 회랑이 연결하며, 전체는 무색입니다.

3. 바리온(§§ 5.6 양성자, 5.7 중성자 참조)
   세 쿼크와 세 회랑이 중앙의 Y 접합으로 모입니다. 핵의 이중선, 파란 위상 호, ‘전이 쿠션’, 원거리장의 가는 선, 동심 그라데이션 등 다른 레이어도 같은 표기를 따릅니다.